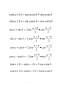Funcții Trigonometrice

Cuprins licență Cum descarc?

Introducere
Capitolul I. Funcţii trigonometrice.
Sisteme de măsură pentru unghiuri şi arce.
Funcţiile trigonometrice sinus, cosinus, tangenta, cotangenta.
Proprietăţile fundamentale ale funcţiilor trigonometrice. 
Capitolul II. Ecuaţii trigonometrice.
Funcţii trigonometrice inverse.
Noţiuni despre ecuaţiile trigonometrice.
Metoda reducerii la ecuaţiile algebrice.
Ecuaţii omogene în raport cu sin⁡x şi cos⁡x.
Metoda introducerii unghiului auxiliar.
Metoda substituţiei universale tg x/2=t.
Metoda substituţiei sin⁡x+cos⁡x=t.
Metoda descompunerii în factori.
Ecuaţii trigonometrice ce conţin modul.
Capitolul III. Aplicaţii. 
Funcţiile trigonometrice ale unghiului ascuţit 
Funcţiile trigonometrice ale unghiului orientat 
Relaţii între funcţiile trigonometrice
Coordonatele polare în plan 
Teorema sinusurilor şi teorema cosinusurilor
Încheierea 
Bibliografia 
Anexe

Extras din licență Cum descarc?

Capitolul I. Funcţii trigonometrice
Sisteme de măsură pentru unghiuri şi arce
În trigonometrie se utilizează două unităţi de măsură a unghiurilor:
Măsura în grade
În acest sistem de măsură unitatea de măsură a unghiului este gradul (1°), definit ca măsura unghiului egal cu a 90-a parte din unghiul drept. Submultiplii săi sunt minutul (1'), egal cu a 60-a parte din grad, şi secunda (1'') – a 60-a parte din minut. Deci 1°=60', 1^'=60''.
Măsura unghiului alungit (desfăşurat) este de 180° (de 2 ori mai mare decât a unghiului drept); măsura unghiului complet (în jurul unui punct) este de 360°. [12, p.155] [5, p.171]
Măsura în radiani
Sistemul de măsură în radiani a unghiurilor are la bază următoarea afirmaţie: raportul dintre lungimea arcului circular, corespunzător unui unghi la centru, şi lungimea razei arcului cercului este o mărime constantă, care nu depinde de rază.
Definiţie: „Fie l lungimea arcului circular de raza r. Numărul α, egal cu raportul dintre lungimea arcului circular şi lungimea razei cercului, se numeşte măsura în radiani a arcului (şi a unghiului la centru corespunzător acestui arc). Astfel α=l/r.”[12, p.155]
Trecerea de la o măsură la alta se realizează folosind faptul că efectuând măsurări ale aceluiaşi unghi (arc) cu două unităţi de măsură diferite se obţin numere, raportul cărora este egal cu raportul unităţilor de măsură respective. Prin urmare, dacă a° este măsura în grade, iar α - măsura în radiani a unui unghi alungit, atunci (a°)/α=(180°)/π, de unde α=(a°)/(180°)∙π rad, a°=α/π∙180°.
[12, p.156]
În continuare prezint exemple:
Exemplul 1: Măsura în radiani (α)a unghiului complet este 2π. Într-adevăr, deoarece lungimea cercului este 2πr, rezultă că α=2πr/r=2π rad, unde π≈3,1416 este un număr iraţional. Măsura în radiani a unghiului alungit este π rad , iar a unghiului drept este π/2 rad. 
[12, p. 155]
Exemplul 2: Transformaţi în radiani măsurile unghiurilor de: 
30°; b) 45°; c) 135°; d) 225°; 
Rezolvare: 
α=(π∙30°)/(180°)=π/6(radiani);
α=(π∙45°)/(180°)=π/4(radiani);
α=(π∙135°)/(180°)=3π/4(radiani);
α=(π∙225°)/(180°)=5π/4(radiani).
Exemplul 3:
Scrieţi în grade măsurile unghiurilor de:
π/5 radiani; b) 5π/6 radiani; c) π/10 radiani; d) π/18 radiani;
Rezolvare:
a°=(180°∙π)/5π=36°;
a°=(180°∙5π)/6π=150°;
a°=(180°∙π)/10π=18°;
a°=(180°∙π)/18π=10°.
[11, p.192]
Funcţiile trigonometrice sinus, cosinus, tangenta, cotangentă
Cerc trigonometric se numeşte cercul de rază l cu centrul în originea sistemului de coordonate.
Lemă: Dacă semidreptele [OM1, [OM2 coincid (M_1≠0, M_2≠0), atunci x_1/y_1 =x_2/y_2 (2), unde M_1 (x_1,y_1), M_2 (x_2,y_2 ) sunt puncte într-un sistem cartezian de coordonate xOy şi y_1∙y_2≠0, (Fig. 1).
Observaţie: Dacă punctul M_1 aparţine cadranului I, rapoartele (2) reprezintă, respectiv, cotangenta, cosinusul, sinusul unghiului ascuţit. Întrucât valorile acestor rapoarte nu depind de lungimea segmentului [〖OM〗_1], ci numai de măsura unghiului format de semidreapta [〖OM〗_1 cu semiaxa pozitivă [Ox, în continuare vom examina numai punctele situate pe cercul trigonometric

Fisiere în arhivă (1):

 Functii Trigonometrice.docx

Imagini din acest licență Cum descarc?

Bibliografie

Lupu, I. Metodica predării matematicii. Chişinău: Editura Liceum, 1996. 308 p. (p. 205-235).
Guatier, C.; Girard, G.; Lentin, A. Algebră. Funcţii numerice, aplicaţii diverse. Bucureşti: Editura Didactică şi Pedagogică, 1973. 439 p. (p. 232-305).
Abramov, A. M.; Ivlev, B. M.; Moiseeva, Z. I. Algebra şi elemente de analiză în clasele 9-10. Chişinău: Editura Lumina, 1984. 335 p. (p. 93-147).
Nicolescu, Cătălin-Petru. Sinteze de matematică. Aplicaţii. Bucureşti: Editura Albatros, 1990. 407 p. (p. 52-58).
Rogai, E.; Rogai, M. Formule şi tabele matematice. Aide-memoire matematic. Bucureşti: Editura Tehnică, 1996. 263 p. (p. 171-196).
Ciobanu, V.; Garit, V.; Lupu, I. Formule matematice. Chişinău: Editura Lumina, 1993.
154 p. (p. 15-25; p. 36).
Gusev, V. A.; Mordcovici, A. G. Matematica. Materie de recapitulare. Chişinău: Editura Lumina, 1988. 274 p. (p. 154-171).
Alecsei, S.; Prodan, N. Consolidarea deprinderilor de rezolvare a problemelor de matematică. Chişinău: Editura Lumina, 1989. 190 p. (p. 169-190).
Bogomolov, N. V.; Serghienco, L. I. Culegere de probleme de matematică. Chişinău: Editura Lumina, 1989. 218 p. (p. 74-93).
Cuculescu, I.; Gaiu, L. N.; Ottescu, C. Matematica. Geometrie, manual pentru clasa VII-a. Bucureşti: Editura Didactică şi Pedagogică, 1998. 174 p. (p. 82-91).
Achiri, I.; Braicov, A.; Ciobanu, M.; Curtescu, T.; Raischi, V. Matematica, manual pentru clasa VIII-a. Chişinău: Editura Prut Internaţional, 2003. 248 p. (p. 181-197).
Achiri, I.; Garit, V.; Poştaru, A.; Prodan, N. Matematica, manual pentru clasa X-a. Chişinău: Editura Prut Internaţional, 2002. 280 p. (p. 155-203).
Achiri, I.; Ciobanu, V.; Efros, P.; Garit, V.; Neagu, V.; Prodan, N.; Taragan, D.; Tapală, A. Matematica, manual pentru clasa XII-a. Chişinău: Editura Prut Internaţional, 2005. 304 p. (p. 262-268).